- Volume 67 , Number 3
- Page: 215–36
SIMLEP: a simulation model for leprosy transmission and control
ABSTRACT
SIMLEP is a computer program for modeling the transmission and control of leprosy which can be used to project epidemiologic trends over time, producing output on indicators such as prevalence, incidence and case-detection rates of leprosy. In SIMLEP, health states have been defined that represent immunologic conditions and stages of leprosy infection and disease. Three types of interventions are incorporated: vaccination, case detection and chemotherapy treatment. Uncertainties about leprosy have led to a flexible design in which the user chooses which of many aspects should be included in the model. These aspects include natural immunity, asymptomatic infection, type distribution of new cases, delay between onset of disease and start of chemotherapy, and mechanisms for leprosy transmission. An example run illustrates input and output of the program. The output produced by SIMLEP can be readily compared with observed data, which allows for validation studies. The support that SIMLEP can give to health policy research and actual decision making will depend upon the extent of validation that has been achieved. SIMLEP can be used to improve the understanding of observed leprosy trends, for example, in relation to early detection campaigns and the use of multidrug therapy, by exploring which combinations of assumptions can explain these trends. In addition, SIMLEP allows for scenario analysis in which the effects of control strategies combining different interventions can be simulated and evaluated.RÉSUMÉ
SIMLEP est un programme informatique conçu pour modéliser la transmission et le contrôle de la lèpre, et qui peut être utilisé pour prévoir les tendances épidémiologiques au cours du temps et produire des indicateurs de tendances comme la prévalence, l'incidence et le taux de détection de nouveaux cas. Au sein du programme SIMLEP, des états de santé ont été prédéfinis, qui représentent des états immunologiques et des grades de l'infection et de la maladie causée par la bacille de la lèpre. Trois types d'intervention sont intégrés: vaccination, détection de cas et traitement chimiothérapeutique. Le programme informatique est flexible pour tenir compte des incertitudes inhérentes à la lèpre, en particulier l'utilisateur peut choisir lesquels de certains aspects doivent être intégrés dans le model. Ces aspects sont l'immunité naturelle, les infections asymptomatiques, le type de distribution des nourveaux cas, le délai entre la déclaration clinique de la maladie et le début de la chimiothérapie, et les mécanismes de transmission de la lèpre. Un example type d'analyse illustre le type de données à entrer et les résultats après analyse et traitement par le programme informatique. Les résultats obtenus par SIMLEP peuvent être facilment comparés avec des données de terrain, ce qui permet de réaliser des études de validation du programme. SIMLEP peut être utilisé en effet pour aider à mieux comprendre les tendances récemment observées dans la lutte contra la lèpre, comme, par example, les campagnes de détection précoces de cas et l'utilisation de la polychimiothérapie, en explorant quelles combinaisons d'hypothèses permettent le mieux d'expliquer ces tendances. Enfin, SIMLEP permet d'analyser des scénarios, dans lesques les conséquences des plans de contrôle de la lèpre, qui combinent des interventions variées, peuvent être simulées et évaluées.RESUMEN
SIMLEP es un programa de computación que permite simular la transmisión y el control de la lepra que peude usarse en el diseno de estúdios epidemiológicos, produciendo indicadores de prevalência, de incidência y de tasas de detección de casos de la enfermedad. En SIMLEP se han definido los estados de salud que rep- resentan las condiciones inmunológicas y los estados de la infección y de la enfermedad. Se incorporan 3 tipos de intervenciones: la vacunación, la detección de casos y el tratamiento por quimioterapia. Las incer- tidumbres sobre la lepra han conducido al desarrollo de un diseno flexible en el cual el usario escoge que aspectos deben ser incluídos en el modelo. Estos aspectos incluyen la inmunidad natural, la infección asin- tomática, el tipo de distribución de los casos nuevos, el retardo entre la aparición de la enfermedad y el inicio del tratamiento, y los mecanismos de transmisión de la lepra. El programa incluye un ejemplo sobre la ali- mentación de datos y los resultados obtenidos. Los resultados producidos por SIMLEP pueden compararse facilmente con los datos observados, lo cual permite estúdios de validación. El apoyo que SIMLEP puede proporcionar y la toma de decisiones dependen dei grado de validación obtenido. SIMLEP puede usarse, por ejemplo, en las campanas de detección de casos y en los programas de tratamiento con poliquimioterapia. Además, SIMLEP permite crear un escenario en el cual los efec- tos de las estrategias de control, combinando diferentes intervenciones, pueden ser simulados y evaluados.Estimates of the short-and long-term effects of leprosy control strategies are required for decision making, for target setting, and for prediction of the moments at which targets are likely to be reached. However, the limited knowledge of leprosy epidemiology and of the effects of population- based interventions make it difficult to explain observed trends in leprosy incidence and morbidity and to predict the future of leprosy.
There is ample evidence that socioeconomic development might affect leprosy transmission, and that secular trends can occur (4, 13). BCG vaccination has a protective effect, but its efficacy is highly variable (5). The introduction of multidrug therapy (MDT) in the 1980s, with its relatively short duration of treatment, resulted world-wide in rapid declines in the prevalence as defined by the number of cases registered for treatment, and MDT has become the mainstay for leprosy control (23). However, convincing evidence for a persistent favorable effect of MDT on new case-detection rates has so far not been observed (6, 22) and, therefore, the long-term impact of MDT-based programs is not clear.
In this situation, simulation models can help to organize knowledge and assumptions on leprosy and to structure discussions on its control. These types of models enable exploration of the behavior of a disease in populations over time under specified assumptions about the processes involved (24). The present paper introduces an epidemiological simulation model for leprosy, SIMLEP, which provides a framework for the quantitative description of the dynamics of leprosy transmission, the course of infection and disease, and the impact of interventions. Simulation results on trends in case-detection rates and in the prevalence of cases registered for treatment can be compared with observed data. SIMLEP can be used to explore the possible effects of interventions such as MDT-based control on leprosy transmission under assumptions or scenarios on unknown aspects of leprosy epidemiology which can be varied by the user.
In the 1970s and 1980s, Lechat, et al. were the first to develop a comprehensive model for leprosy (15-19'). Their simulations concentrated on the comparison of the long- term impact of alternative control strategies, and helped considerably to clarify the thinking about leprosy control. SIMLEP builds on the approach which is followed in the Lechat model and in several conceptually similar tuberculosis models (1-3, 26, 30). Shortly after the introduction of MDT- based control, Lechat, et al. made a courageous attempt to explore its consequences (l6-18). However, their predicted rapid and persisting decline in incidence has not been observed in reality. In its conclusions and recommendations, the 1991 International Meeting on Epidemiology of Leprosy in Relation to Control recognized a need for making predictions for future trends, and recommended that simulation models should be developed (11). This has initiated the development of the present SIMLEP model. SIMLEP allows for variation of many model assumptions, for example, with respect to natural immunity, the incubation period and asymptomatic infection. Delays for becoming aware of disease and for start of treatment are incorporated, and SIMLEP also provides different mechanisms for describing leprosy transmission. SIMLEP includes detailed output facilities for comparison of simulation results with observed trends, and for the prediction of future trends.
This paper describes the structure of the SIMLEP model, gives an example of a SIMLEP simulation experiment, and discusses quantification of the model, potential applications and known limitations. Background information on simulation modeling for tropical diseases, and for leprosy in particular, can be found elsewhere (9-l0-15-24). The Annex gives a mathematical description of SIMLEP. More detailed information on SIMLEP is provided in the manual (21).
SIMLEP model
The SIMLEP model describes the process of leprosy transmission, disease and control in a population which is followed over time. SIMLEP has a pre-defined structure of compartments (representing health conditions with respect to leprosy) and flows between compartments (Fig. 1). Within this framework, the SIMLEP user can specify assumptions about demography, leprosy and interventions by giving birth and death rates and numerical specifications for the flows between the compartments. The arrows with solid shafts and points in Figure 1 represent birth, death and the flows (transitions) between the compartments (boxes in the flowchart). The dashed arrows with open heads-or influence arrows-and the "force of infection circle" represent leprosy transmission. The arrows with solid shafts and heads indicate flows related to the SIMLEP interventions: vaccination, case detection and chemotherapy. By not using boxes-0% flows-the user can simplify the model actually used. SIMLEP performs all calculations for each age separately, and represents the epidemiological situation at the end of a simulation time step by the age-specific distribution of the population over the various compartments. The maximum value for the time step in SIMLEP simulations is 2 months. Flows from compartments are calculated according to (Markov) transition rates if not indicated otherwise. A flow between two compartments, say k and l, is indicated by fkl (both k and l run from a to j; Fig. 1). The three flows f0a, f0b and f0c. represent births, and death from a compartment, say m, is denoted by fmz (m runs from a to j).
Background situation. The history of leprosy control influences future trends of leprosy in an area and is, therefore, simulated in SIMLEP. SIMLEP runs always start from a stable situation, i.e., an age-specific distribution of the population over the various compartments in which no changes over time occur, with all control measures switched off. This stable situation is derived from the numerical specifications for the model parameters and from a user-specified background incidence rate for the first years of interest for the simulation run (incidence being defined as the first appearance of any specific signs or symptoms of leprosy). SIMLEP will automatically fit this background incidence rate at the start of a simulation experiment by tuning the transmission parameter β (defined later).
Demography. Birth is simulated according to a crude birth rate. A life table governs death in SIMLEP: at the end of each time step, age-specific death rates which correspond to the life table are applied (flows faz, fbz, . . ., fjz,) and the age structure of the population is updated. S1MLEP does not consider migration and possible excess mortality in leprosy patients, and does not distinguish between males and females.
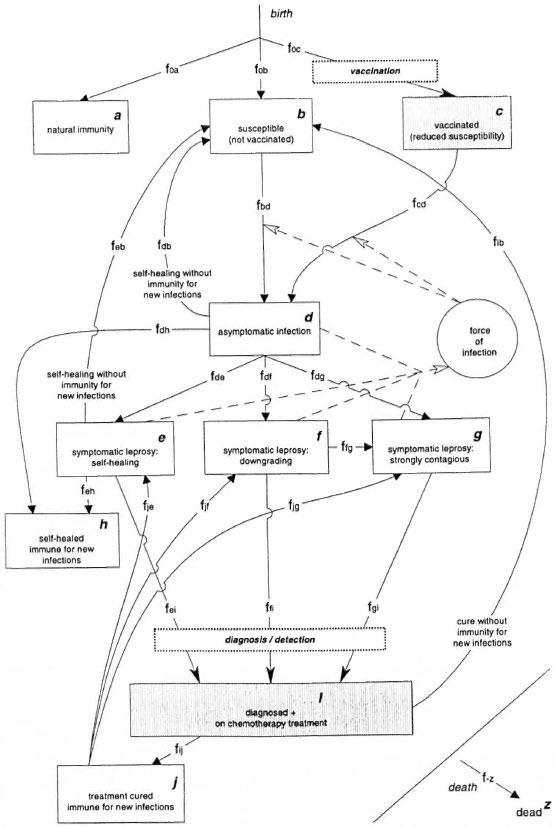
Fig. 1. SIMLEP: The health states (compartments), the flows between them (arrows), the process of leprosy transmission (dashed arrows and "force of infection" circle) and two interventions: vaccination and diagnosis plus chemotherapy ("intervention" flows and shaded compartments). All transitions are age-specific and the age structure of all compartments is updated at the end of each simulation time step.
Susceptibles and nonsusceptibles. In order to evaluate the potential impact of natural immunity against leprosy, SIMLEP has the option to specify a fraction of newborns to enter the compartment of life-long natural immunity (flow f0a). The other newborns all enter the compartment susceptible (flow f0b). The compartment susceptible can also contain individuals who were cured after treatment without acquiring immunity against new leprosy infections. Upon acquiring a leprosy infection, people from the SUSCEPTIBLE compartment move to the compartment ASYMPTOMATIC INFECTION (flow fbd).
Course of infection and disease. In SIMLEP, infected individuals are assumed to pass first through an episode without manifestation of specific signs or symptoms of leprosy, which is represented by the compartment ASYMPTOMATIC INFECTION. The user can specify time distributions for the length of this episode (see the Annex). SIMLEP offers the possibility of spontaneous healing of asymptomatic infections without manifestation of symptomatic leprosy (flows fdb and fdh). Flows fde, fdf and fdg denote the first appearance of any sign or symptom of leprosy (e.g., skin lesion or nerve function impairment) irrespective of recognition by the patient or diagnosis by a medical worker. SIMLEP distinguishes three expression types of symptomatic leprosy: 1) symptomatic leprosy from which all individuals will self-heal when left untreated (via a self-healing rate; flows feb and feh): SELF-HEALING SYMPTOMATIC LEPROSY; 2) symptomatic leprosy that is not strongly contagious, but from which individuais will downgrade to STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY at a later stage when left untreated (via a downgrading rate; flow ffg ): DOWNGRADING SYMPTOMATIC LEPROSY; and 3) symptomatic leprosy that is strongly con-tagious directly upon manifestation of thefirst signs or symptoms of leprosy: STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY.
Note that preventing downgrading will enhance the impact of early detection and chemotherapy on transmission. For evidence of downgrading see Scott, et al. (27). After self-healing from asymptomatic infection or symptomatic leprosy, people either are susceptible to a new infection and move to SUSCEPTIBLE (flows fdb and feb), or become immune and move to SELF-HEALED & IMMUNE FOR NEW INFECTIONS (flows fdh and feh). Possible endogenous reactivation of leprosy in self-healed individuals is neglected. People with symptomatic leprosy move to the compartment DIAGNOSED + ONCHEMOTHERAPY TREATMENT as soon as they are detected and are put on treatment.
Transmission. New infections (flows fbd and fed) are assumed to be caused by contagious individuals in the population. Knowledge on who are responsible for leprosy transmission, and to what extent, is limited. It cannot be excluded, for example, that most transmission occurs in the episode of asymptomatic infection. In SIMLEP, contagiousness is therefore modeled in a flexible way; it can be switched on and off separately for: 1) each of the four groups in compartment ASYMPTOMATIC INFECTION, namely, the ones who self-heal without becoming symptomatic, and the people later becoming symptomatic of, respectively, the self-healing, downgrading and strongly contagious types; 2) people in compartment SELF-HEALING SYMPTOMATIC LEPROSY and 3) people in compartment DOWNGRADING SYMPTOMATIC LEPROSY.
A person with STRONGLY CONTAGIOUSSYMPTOMATIC LEPROSY is assumed always to be contagious, but he might rapidly infect people living close to him. After some time, this person will therefore have transmitted Mycobacterium leprae to most of his susceptible contacts. To account for this, the capability to transmit M. leprae gradually decreases over time (it follows a negative exponential function) for all persons who enter the compartment STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY. This loss of contagiousness can be quantified by the average contagiousness-closs-of all people in the compartment STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY relative to the level of contagiousness at entry in this compartment.
For the compartments for which contagiousness is optional (ASYMPTOMATIC INFECTION, SELF-HEALING SYMPTOMATIC LEPROSY, DOWNGRADING SYMPTOMATIC LEPROSY), the user should specify a second (lower) level of contagiousness relative to the initial level in the compartment STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY. Because of this lower level, SIMLEP does not postulate loss of contagiousness for the compartments SELF-HEALING SYMPTOMATIC LEPROSY and DOWNGRADING SYMPTOMATIC LEPROSY. Presently, the simplifying assumption has been made that the duration of the episode of asymptomatic infection is following the same time distribution for those who self- heal without development of symptoms and for those who proceed to symptomatic leprosy of either the self-healing or the downgrading type. A different time distribution can be specified for those who proceed to STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY. The contagiousness in compartment ASYMPTOMATIC INFECTION is assumed to build up gradually to the level of strong contagiousness for those who move to STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY, and to the second (lower) level of contagiousness for those who do not.
SIMLEP translates the (weighted) contagiousness of all contagious people together into the force of infection (circle in Fig. 1) which is the rate at which individuals who are still susceptible acquire M. leprae infection (flow fbd). For example, if only people in the compartment DOWNGRADING SYMPTOMATIC LEPROSY are contagious in addition to the people from the compartment STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY then the force of infection FOI is equal to
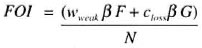
| β | = | with closs as in above text and measure for contagiousness of people who just entered the compartment STRONGLY CONTAGIOUS SYMPTOMATIC LEI'ROSY |
| wweak | = | weighting factor: the level of contagiousness in the compartments SELF-HEALING SYMPTOMATIC LEPROSY and DOWNGRADING SYMPTOMATIC LEPROSY is given by wweak β |
| F | = | number of people in the DOWNGRADING SYMPTOMATIC LEPROSY |
| G | = | number of people in the compartment STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY |
| N | = | total population size. |
The fraction among the susceptible people that acquires M. leprae infection during a simulation time step (Δt) is calculated from this force of infection and equals FOI Δt. If other compartments are also (weakly) contagious, the people in these compartments are added to the FOI term. The gradual buildup of contagiousness in the compartment ASYMPTOMATIC INFECTION is described in more detail in the Annex. Secular declines in leprosy can be taken into account by an annual reduction factor for the transmission parameter β.
Leprosy control. Vaccination. BCG vaccination is often given in early childhood. It only offers protection to a certain degree (5). In SIMLEP, vaccination is assumed to take place at birth with a user-defined coverage. Vaccinated newborns without natural immunity enter the compartment VACCINATED (REDUCED SUSCEPTIBILITY) (flow foc). People in this compartment can still be infected but at a lower rate (flow fed). In a study in South India, the protective efficacy of BCG for younger ages decreased from 58% to 18% over a period of 15 years (7). The protective efficacy can therefore be specified to depend on the time since vaccination.
Diagnosis. Early case detection reduces the delay between onset of symptomatic leprosy and start of chemotherapy. In SIMLEP, this delay consists of two consecutive parts: cases must first become aware of their disease ("awareness delay") before they can look for care after a certain "reporting delay." The user specifies case detection by choosing two rates which are associated with the awareness delay and the reporting delay, respectively. A reporting delay which is infinitely long corresponds with absence of treatment.
Chemotherapy. Chemotherapy shortens the average duration of contagiousness of patients. It is believed that with rifampin bacterial kill is achieved almost instantaneously at the first dose, and that dapsone monotherapy can achieve this effect in about 3 months. However, for simplification, both dapsone monotherapy and multidrug therapy are in SIMLEP assumed to start at the moment of diagnosis and to immediately stop the contagiousness of patients.
Upon starting treatment, patients move to the noncontagious compartment DIAGNOSED + ON CHEMOTHERAPY TREATMENT (flows fei, ffi and fgi). The duration of leprosy treatment depends on the type of leprosy at presentation. In SIMLEP, one average treatment duration must be specified per treatment regimen, reflecting the mean treatment duration over the different types of symptomatic leprosy. This duration is converted into a treatment cessation rate; treatment cessation thus does not depend on the bacteriological status of patients. Fixed durations of treatment were not implemented in SIMLEP because of computational complexities. In view of the possibility of endogenous reactivation after cessation of treatment, provision is made for relapses. A new infection can also cause a new episode of symptomatic leprosy after cessation of treatment. In SIMLEP, both options are offered: after cessation of treatment, a fraction can return to the compartment susceptible (flow fib), and a fraction can move to the compartment TREATMENT
CURED & IMMUNE FOR NEW INFECTIONS (flow fij) from which they can experience a relapse to the compartments for symptomatic leprosy (flows fie, fjf, fjg).
A chemotherapy-based control strategy in SIMLEP is characterized by the awareness delay, the reporting delay, the duration of treatment, and relapse rates (if relapses are specified to occur) which are specific for the type of treatment used (dapsone monotherapy or multidrug therapy). Note that since both dapsone and multidrug therapy are assumed to immediately stop the contagiousness of patients, only shorter associated delays in diagnosis and lower relapse rates can render multidrug therapy-based control to be more powerful in reducing transmission than dapsone-based control. Upon cure, individuals either become immune or susceptible for new infections. The corresponding fractions are in SIMLEP independent of the type of treatment. Thus, they are identical for dapsone monotherapy and multidrug therapy. Up to six chemotherapy control strategies can be applied consecutively in one simulation run.
Example
An example of a simulation run is discussed below in order to show how SIMLEP can be used. As an illustration, a model structure and a set of parameter quantifications have been chosen that in our judgment are not implausible. A simplified model with no NATURAL IMMUNITY (no f0a) and with self-healing and treatment cure always being followed by immunity (no fdb, feb, and fib) is used (Fig. 2). The parameter quantifications for demography, transmission, course of infection and disease and control strategies are listed in Tables 1 and 2. In the text below, figures in parentheses denote choices for parameter quantifications.
Input specifications. The stable epidemiological situation at the start of the simulation (1950) has an incidence rate of 2 per 1000 population per year. Demographic data for India for 1976 were used for the birth rate (34.4 per 1000 population) and the life table (Health Monitor, Pune, India: The Foundation for Research in Health Systems, 1993, pp. 10, 21). In SIMLEP, the birth rate and life table simulate populations with a constant growth rate and age structure.
By excluding natural immunity, it is assumed that everyone can develop leprosy. The duration of asymptomatic infection is, on average, shorter for those who will not directly develop STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY than for those who will (Fig. 3). The average durations are 6.8 and 13.4 years, and the probabilities for this episode to be shorter than 5 years are 73% and 37%, respectively.
Of newly infected individuals, a fraction will self-heal without developing symptomatic leprosy (30%), while the others (70%) will develop symptomatic leprosy. Recovery from an asymptomatic infection, self-healing from symptomatic leprosy, and cure by treatment are assumed to lead to immunity for new leprosy infections (exclusion of flows fdb, feb, and fib). The proportion among new symptomatic cases developing strong contagiousness de novo is relatively small (10%), and cases downgrading at a later stage (30%) will make an important contribution to the pool of strongly contagious individuals. The average duration until self-healing from symptomatic leprosy of 3 years implies that 33% per year will self-heal. Similarly, the annual downgrading rate is 20% per year (or 5 years on average).
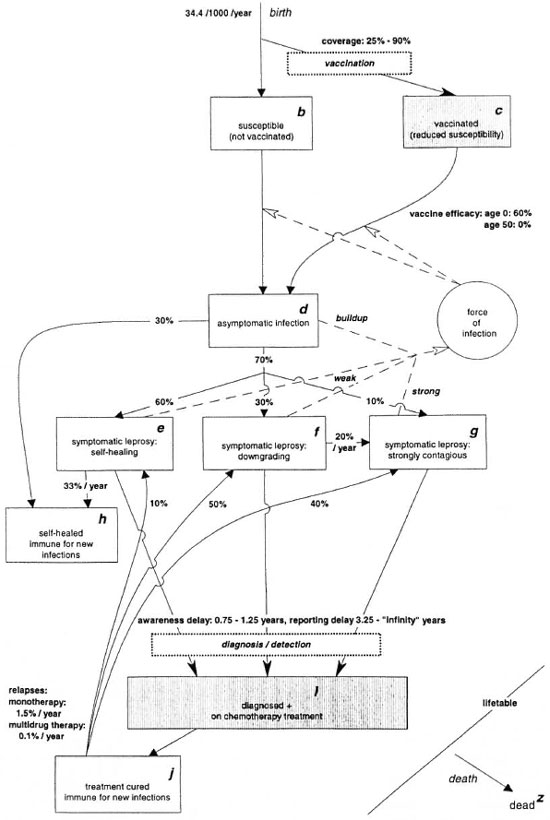
Fig. 2. Example: Model structure (all ages combined) and parameter specifications.

All individuals in the compartment asymptomatic infection are building up contagiousness, and all untreated symptomatic leprosy cases who are not of the STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY type are weakly contagious. Their relative degree of contagiousness (9%) was calculated in such a way that STRONG CONTAGIOUS SYMPTOMATIC LEPROSY cases in total infect four times as many individuals as self-healing cases. In SIMLEP, the strongly contagious cases become gradually less effective in transmitting M. leprae (the effectiveness reduces by 50% every 9 months). A "natural" decline in the trend of leprosy incidence is not assumed in the simulation.
The assumptions on leprosy control are summarized in Table 2. BCG, which is administered at birth, has a protective efficacy which by assumption decreases from 60% at age 0 to 0% at age 50 and over. Vaccination starts in 1980, and the coverage increases from 25% in the period 1980-1989 to 75% in 1990 and further to 90% from 1995 onward.
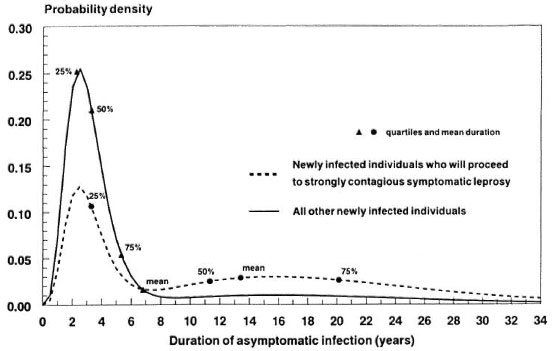
Fig. 3. Example: Probability density functions for the duration of ASYMPTOMATIC INFECTION for those who after this episode directly will proceed to STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY (the probabilities for this episode to be shorter than 5, 10 and 20 years are, respectively, 37%, 47% and 75%) and those who either will self-heal without showing any sign or symptom of leprosy or will proceed to another expression type of symptomatic leprosy (the corresponding probabilities are 73%, 82% and 92%, respectively).
Case detection plus chemotherapy start in 1955. A buildup phase of 5 years is assumed for case detection. The program remains unchanged in the period 1960-1990. The years 1990-1993 reflect a transition phase from dapsone to multidrug therapy during which both the awareness delay and the reporting delay are reduced. The delays again remain unchanged from 1993 onward; see Figure 4 for the probability distribution of the total delay. It has a high variability, with probabilities of 17%, 43%, 86% and 99% that the delay is smaller than 1, 2, 5 and 10 years, respectively. These values apply to all three types of symptomatic leprosy.
The average durations of dapsone treatment, of multidrug therapy, and of the shortened duration of MDT treatment which is postulated from 1998 onward are based on the mix of the different types of symptomatic leprosy considered (the average durations are associated with negative exponential time functions that correspond with treatment completion rates). As mentioned above, cure by treatment in this example implies immunity for new infections (exclusion of flow fib). Relapse rates after dapsone monotherapy (1.5% per year) are much higher than after multidrug therapy (0.1 % per year). The distribution of relapses over the three types of symptomatic leprosy (10%, 50%, 40%) is in SIMLEP independent of the administered therapy (dapsone monotherapy or multidrug therapy).
Simulation results. The user interface of SIMLEP enables on screen inspection and printing of the output of simulations in both tabular form and through a large number of pre-defined graphs. The pre-defined graphs include both type- and age-specific graphs for the rates of onset of symptomatic leprosy (incidence rate) and of starting chemotherapy treatment of symptomatic leprosy, and for the point prevalences of untreated symptomatic cases and of symptomatic cases on treatment.
Figure 5 shows, for the example run, aslow but persistem decrcase in the incidence rate from the gradual introduction of dapsone-based control in 1955-1960 onward. The rate of decline increases shortly after 1990 because of the introduction of multidrug therapy and the rise in BCG coverage. The introduction of multidrug therapy is associated with less opportunities for the transmission of M. leprae due to a (somewhat) earlier detection and its lower relapse rate (relapsed cases contribute to transmission until they again start treatment). The number of cases relapsing after treatment is small as compared to the number of incidence cases. In SIMLEP, case detection only counts when a chemotherapy treatment is started. The early peak in treatment starting rates reflects a clearance of a backlog of untreated cases from the pre- control era. The increase in the treatment starting rate in the transition phase toward multidrug-based control (1990-1993) is explained by earlier detection due to an assumed shortening of the awareness and reporting delays. As a consequence, the gap between the treatment starting rate and the incidence rate becomes smaller (Fig. 5), and the prevalence of untreated cases declines (Fig. 6).

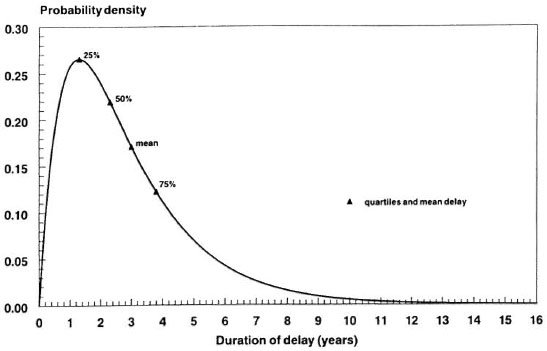
Fig. 4. Example: Probability density function for the total delay between onset of the first sign or symptom of leprosy and start of chemotherapy during the chemotherapy control strategy over the years 1993-2020 in the example.

Fig. 5. Example: Simulated incidence rate of symptomatic leprosy, rate of starting treatment and relapse rate (all expression types of symptomatic leprosy combined).
In the pre-control period, STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY is life-long. Excess mortality due to leprosy is in addition not (yet) included in SIMLEP. The resuiting accumulation is the cause of the high prevalence of over 23 per 1000 total population in the pre-dapsone era (Fig. 6). The clearance of the prevalence pool after the introduction of dapsone gives a rapid fall in the prevalence of untreated cases in the period 1955-1965. Further falls in the total prevalence and in the prevalence of cases on treatment in 1989-1990 and again in 1997-1998 are explained by the sudden decreases in the duration of treatment. These reductions lead to less resource requirements and workload in the control program. In the example, the incidence rate (Fig. 5) and the prevalence of untreated cases (Fig. 6) are not decreasing very fast, especially because individuals in the compartment ASYMPTOMATIC INFECTION build Up contagiousness before diagnosis takes place.

Fig. 6. Example: Simulated point prevalences of untreated symptomatic leprosy, of cases on treatment, and "total" (all types of symptomatic leprosy combined).
DISCUSSION
In developing the SIMLEP simulation model we made choices regarding aspects to be included and their level of detail, keeping in mind the objectives of SIMLEP: to be a useful tool in analyzing leprosy data and, in particular, to be valuable in predicting the effects of existing and potential control policies.
Both objectives require characterization of processes underlying leprosy transmission. Several aspects relating to susceptibility and transmission are included: natural immunity, asymptomatic infections, differences in contagiousness between asymptomatic and symptomatic stages, and the decline in effective contagiousness over time. This decline reflects that household and other frequent contacts of highly contagious cases are probably already infected during the period shortly after the index case became contagious.
A central issue is the impact of control on transmission. Control options can be described while taking into account the limitations in their effectiveness. When specifying a SIMLEP vaccination program, one may account for incomplete coverage, less than 100% protective efficacy, and waning of protection over time. The influence of a control program on case detection can be simulated by its impact on two consecutive delays. The delays can be thought to represent becoming aware of leprosy symptoms and reporting the disease, respectively. The delays may, for example, decrease when short-term chemotherapy is introduced. Provisions for relapse and for susceptibility to new infections following cure limit the effectiveness of chemotherapy control. SIMLEP produces output on trends in age- specific prevalence, incidence and case-detection rates in order to study the impact of the interventions vaccination, case detection and chemotherapy treatment.
SIMLEP can assist in clarifying the basic mechanisms that govern transmission and the natural history of leprosy as well as the impact of control. One could argue that the present structure of SIMLEP is too complex for this type of application. However, the user may simplify the model structure within the SIMLEP framework according to his or her requirements. By selectively inactivating flows and compartments from the full SIMLEP structure, much simpler models can be simulated. For example, it is possible to simulate chemotherapy control strategies using a model with only the five compartments SUSCEPTIBLE, ASYMPTOMATIC INFECTION, SELF-HEALING SYMPTOMATIC LEPROSY, STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY and DIAGNOSED + ON CHEMOTHERAPY TREATMENT of Figure 1.
On the other hand, SIMLEP may not be sufficiently comprehensive. Model extensions that are required when specific questions are addressed may often be incorporated in SIMLEP. Examples are: excess mortality, separate contagiousness of self- healing infections, drug resistance and prolonged contagiousness after initiation of chemotherapy. The same applies to the distinction between males and females which is not yet included. But increasing the number of aspects covered in a compartment model such as SIMLEP quickly leads to an explosion of the number of states in the computer program, leading to unrealistic requirements regarding computer power. The population-based simulation of compartments also prohibits incorporation of certain aspects. This particularly applies to provisions for explicit and detailed modeling of high transmission risks in small groups such as households, or detailed modeling of individual (genetic/hereditary) differences in susceptibility, which require individual based simulation. Note that these kinds of heterogeneity can substantially influence the age distribution of prevalence, incidence and case detection rates, and the impact of interventions on transmission.
Quantification and validation. Proper validation of a model is crucial for its usefulness as a tool for prediction, evaluation, and planning. Uncertainty about the validity of SIMLEP refers to both the structure of the model and to the quantification of the individual parameters, and reflects the state of knowledge on leprosy. This uncertainty is shared with any other approach to produce statements on leprosy epidemiology and its control. Levels of uncertainty about model parameters vary with the amount and quality of pertinent data that can be used for testing and quantifying assumptions. The age structure and life table can be obtained from demographic data which are available for most regions. Program registries give information on the type distribution of new symptomatic cases according to type of leprosy at the time of detection. Relapse rates after cure by dapsone monotherapy and multidrug therapy have been documented (32). Some data are also available on self- healing and downgrading rates (27, 28). Crude estimates on delays between onset of disease and start of chemotherapy have been obtained in several control programs by interviewing patients (20, 25, 29, 31). Vaccine trials give information on the extent to which vaccines can prevent new cases of leprosy (5).
There are also parameters for which it is much more difficult, if not impossible, to collect data. Due to a lack of diagnostic tools to establish M. leprae infection, knowledge is in particular limited on the incubation period, on the occurrence of asymptomatic infections and natural immunity, and on leprosy transmission. The flexibility in SIMLEP can be used to explore and test a broad range of assumptions about transmission. The example can be used to illustrate that different combinations of assumptions may describe trend data equally well. We assumed that natural immunity does not occur, and that all individuals who have asymptomatic or symptomatic leprosy infections are contagious. However, the incidence rates in the pre-control period and in 1990, as shown in Figure 5, can also be obtained when 80% natural immunity is assumed among newborns or when contagiousness is assumed to be restricted to strongly contagious leprosy cases only, with simultaneous adaptation of transmission parameters, such as the level of weak contagiousness, the half-life time of the effectiveness in transmitting M. leprae for strongly contagious individuals, and the contagiousness of a strongly contagious individual as expressed by SIMLEP's internal transmission parameter β.
Further confidence in the model is to be gained from extensive validation studies in which detailed data sets are being used. At present, SIMLEP is being validated on the long-term data describing the decline of leprosy in Norway between 1850 and 1920 (12). Model assumptions will be checked against age-specific information on trends in prevalence, incidence and case detection of leprosy by calendar year and birth cohort, using available information on the reporting delay and on changes in the proportions of patients being isolated. Trends will be analyzed for areas with different initial endemicity levels in 1850.
The mid-term and long-term impact of intensified case finding plus MDT on leprosy transmission is still unclear. The transition phase from dapsone-based to MDT- based programs often goes hand in hand with intensification of case detection efforts, which may lead to increasing new case detection rates, even if incidence rates are declining. Benefits of this change in policy in terms of reductions in leprosy transmission may also not directly be visible due to the long incubation period of leprosy. Further validation studies will be targeted at describing the impact of leprosy control (including BCG vaccination). The uncertainty about model assumptions, especially relating to leprosy transmission, can potentially be narrowed down by comparing SIMLEP results with data from recent intervention studies (5, 8, 4). These further validation studies are essential in making SIMLEP a useful tool for prospectively evaluating alternative intervention policies.
Contribution to policy discussion. Policy makers and epidemiologists face large gaps in knowledge about leprosy. Still, policy makers have to make decisions about leprosy control, and epidemiologists and leprosy experts are sometimes tempted to make quite forthright forecasts on future incidence and prevalence of leprosy (23). The SIMLEP example tried by us suggests that it may not be easy to achieve rapid declines in leprosy transmission through intensified case finding plus MDT. In situations like this that are fraught with uncertainties, a simulation model like the present SIMLEP can be a useful, independent input in rational reasoning about leprosy. When experts and decision makers specify their knowledge and uncertainties about aspects of leprosy, the model can be used to predict the range of possible effects of these options. In future, we will analyze how sensitive predictions of trends and the effects of control policies are for variation in the input parameters, and will identify those uncertain parameters that affect the predictions most.
Acknowledgment. SIMLEP was developed in a collaborative project between Erasmus University Rotterdam, Rotterdam, The Netherlands, and the CJIL Field Unit, Chennai, India. The input of participants of the ICMR-WHO workshop on "Simulation Modeling in Leprosy" (Chennai, 1994) and of the members of the Leprosy Prevention Trial Study Group and Leprosy Vaccine Trial Study Group (ICMR) has greatly contributed to the development of SIMLEP. Financial support for this project by the Netherlands Leprosy Relief (NSL) and the WHO Division of Action Programme for the Elimination of Leprosy is gratefully acknowledged.
REFERENCES
- Acocella, G., Pollini, W., Pelati, L., Nonis, A., Gialdroni-Grassi, G. and Grassi, C. Eskimo: an epidemiological simulation kinetic model for tuberculosis. G. Ital. Chemioter. 36 (1989) 1-10.
- Azuma, Y. A simple simulation model of tuberculosis epidemiology for use without large-scale computers. Bull. WHO 52 (1975) 313-322.
- Brogger, S. Systems analysis in tuberculosis control: a model. Am. Rev. Resp. Dis. 95 (1967) 419.
- Fine, P. E. Reflections on the elimination of leprosy. (Editorial) Int. J. Lepr. 60 (1992) 71-80.
- Fine, P. E. and Smith, P. G. Vaccination against leprosy-the view from 1996. (Editorial) Lepr. Rev. 67 (1996) 249-252.
- Gupte, M. D. Elimination of leprosy: forecasts and projections. Indian J. Lepr. 66 (1994) 19-35.
- Gupte, M. D. Field trials of antileprosy vaccines. (Editorial) Indian J. Lepr. 70 (1998) 363-367.
- Gupte, M. D., Vallishayee, R. S., Ananthara- man, D. S., Nagaraju, B., Sreevatsa, Balasub- ramanyam, S., de Britto, R. L. J., Elango, N., Uthayakumaran, N., Mahai.ingam, V. N., Lour- dusamy, G., Ramalingam, A., Kannan, S. and Arokiasamy, J. Comparative vaccine trial in South India. Indian J. Lepr. 70 (1998) 369-388.
- Habbema, J. D., De Vlas, S. J., Plaisier, A. P. and van Oortmarssen, G. J. The microsimulation approach to epidemiologic modeling of helminthic infections, with special reference to schistosomiasis. Am. J. Trop. Med. Hyg. 55 (1996) 165-169.
- Habbema, J. D., Jozefzoon, E. and van Oort- marssen, G. J. Towards the use of decision sciences in leprosy control. Lepr. Rev. 63 Suppl. (1992) 48s-52s.
- International meeting on epidemiology of leprosy in relation to control held in Jakarta, Indonesia, 17-21 June 1991. Lepr. Rev. 63 Suppl. (1992) 1s-126s.
- Irgens, L. M. Leprosy in Norway; an epidemiological study based on a national patient registry. Lepr. Rev. 51 Suppl. 1 (1980) i-xi, 1-130.
- Irgens, L. M. and Skjaerven, R. Secular trends in age at onset, sex ratio, and type index in leprosy observed during declining incidence rates. Am. J. Epidemiol. 122 (1985) 695-705.
- Karonga Prevention Trial Group. Randomised controlled trial of single BCG, repeated BCG, or combined BCG and killed Mycobacterium leprae vaccine for prevention of leprosy and tuberculosis in Malawi. Lancet 348 (1996) 17-24.
- Lechat, M. F. Epidemiometric modeling in leprosy based on Indian data. Lepr. Rev. 63 Suppl. (1992) 31s-39s.
- Lechat, M. F„ Deci.ercq, E. E„ Misson, C. B. and Vellut, C. M. Selection of MDT strategies through epidemiometric modeling. Int. J. Lepr. 58 (1990) 296-301.
- Lechat, M. F„ Misson, C. B„ Lambert, A., Bouckaert, A., Vanderveken, M. and Vellut, C. Simulation of vaccination and resistance in leprosy using an epidemiometric model. Int. J. Lepr. 53 (1985) 461-467.
- Lechat, M. F., Misson, C. B., Vanderveken, M„ Vellut, C. M. and Declercq, E. E. A computer simulation of the effect of multidrug therapy on the incidence of leprosy. Ann. Soc. Belg. Med. Trop. 67 (1987) 59-65.
- Lechat, M. F., Misson, J. Y„ Vellut, C. M„ Misson, C. B. and Bouckaert, A. Un modèle épidémiométrique de la lèpre. Bull. WHO 51 (1974) 361-373.
- Li, H. Y„ Pan, Y. L. and Wang, Y. Leprosy control in Shandong Province, China, 1955-1983; some epidemiological features. Int. J. Lepr. 53 (1985) 79-85.
- Meima, A., Gupte, M. D. and Habbema, J. D. A guide to SIMLEP: a simulation modeling computer program for epidemiology and control of leprosy. Rotterdam: Department of Public Health, Erasmus University Rotterdam, 1998 (in press).
- Meima, A., Gupte, M. D., van Oortmarssen, G. J. and Habbema, J. D. Trends in leprosy case detection rates. Int. J. Lepr. 65 (1997) 305-319.
- Noordeen, S. K. Elimination of leprosy as a public health problem: progress and prospects. Bull. WHO 73 (1995) 1-6.
- Remme, J. E. Epidemiological modeling for tropical disease control. Lepr. Rev. 63 Suppl. (1992) 40s-47s.
- Schreuder, P. A. The occurrence of reactions and impairments in leprosy: experience in the leprosy control program of three provinces in northeastern Thailand, 1987-1995. I. Overview of the study. Int. J. Lepr. 66 (1998) 149-158.
- Schulzer, M., Radhamani, M. P., Grzybowski, S., Mak, E. and Fitzgerald, J. M. A mathematical model for the prediction of the impact of HIV infection on tuberculosis. Int. J. Epidemiol. 23 (1994) 400-407.
- Scott, G. C„ Russell, D. A., Boughton, C. R. and Vincin, D. R. Untreated leprosy: probability for shifts in Ridley-Jopling classification; development of "flares," or disappearance of clinically apparent disease. Int. J. Lepr. 44 (1976) 110-122.
- Sirumban, P., Kumar, A. andNEEi.an, P. N. Healing time in untreated paucibacillary leprosy: a cross- sectional study. Int. J. Lepr. 56 (1988) 223-227.
- Smith, T. C. and Richardus, J. H. Leprosy trends in northern Thailand: 1951-1990. Southeast Asian J. Trop. Med. Public Health 24 (1993) 3-10.
- Waaler, H. T. A dynamic model for the epidemiology of tuberculosis. Am. Rev. Respir. Dis. 98 (1968) 591-600.
- Wittenhorst, B„ Vree, M. L„ Ten Ham, P. B. and Velema, J. P. The National Leprosy Control Programme of Zimbabwe: a data analysis, 1983-1992. Lepr. Rev. 69 (1998) 46-56.
- WHO Leprosy Unit. Risk of relapse in leprosy. Geneva: World Health Organization, 1994. WHO/CTD/LEP/94.1.
1. M.Sc.; Department of Public Health, Faculty of Medicine, Erasmus University Rotterdam, P.O. Box 1738, 3000 DR Rotterdam, The Netherlands.
2. Ph.D.; Department of Public Health, Faculty of Medicine, Erasmus University Rotterdam, P.O. Box 1738, 3000 DR Rotterdam, The Netherlands.
3. Ph.D., Department of Public Health, Faculty of Medicine, Erasmus University Rotterdam, P.O. Box 1738, 3000 DR Rotterdam, The Netherlands.
4. M.D., D.P.H., CJIL Field Unit, and Institute for Medical Statistics, Indian Council of Medical Research, Chennai, India.
Reprint requests to A. Meima at the above address or FAX: 31-10-408-9449; e-mail: Meima@mgz.fgg.eur.nl
Received for publication on 11 June 1998.
Accepted for publication in revised form on 24 May 1999.
ANNEX
Tliis annex gives a complete description of the SIMLEP model. Compartment names in this annex refer to the flowchart (Figure 1) and arc given in capital. Some compartments have been split up in sub-compartments in order to allow sojourn time distributions other than negative exponential and in order to allow the effectiveness of contagiousness to reduce over time. A complete set of equations describing the model is given at the end of this Annex.
The sub-compartments Dij (i=I,2,j=l,..5), E1, E2, F1, F2, G1, G2, G3, G4. J1 and f2
Upon infection, individuals enter the compartment D which represents the asymptomatic period. This compartment is divided into two parallel chains of five successive stages (sub-compartments) with equal transition rates within each chain. This results in ten sub-compartments Dij (i=1, 2J=1,..5) with two transition rates λi (i=l,2).
The compartments SELF-HEALING SYMPTOMATIC LEPROSY (E) and DOWNGRADING SYMPTOMATIC LEPROSY (F) have been split up in E1 and F1 for individuals who are not (yet) aware of their disease, and E2 and F2 for individuals who have become aware of their disease. The compartment STRONGLY CONTAGIOUS SYMPTOMATIC LEPROSY (G) is also subdivided to allow for individuals who are and who arc not aware of their disease. In addition, G is further subdivided into a category in wliich contagiousness is still fully effective, and a category for individuals with zero effectivity in traasmitting M. leprae. Thus, G consists in fact of the following four sub-compartments:
G1 not aware of disease, full effectivity of contagiousness
G2 not aware of disease, zero effectivity of contagiousness
G3 aware of disease, full effectivity of contagiousness
G4 aware of disease, zero effectivity of contagiousness.
Individuals shift from full to zero effectivity of contagiousness with a transition rate λfoi loss. The average contagiousness closs of all people in G (see main text) is the weighted average of the effectivity of contagiousness of individuals in the compartments G1 and G3 (full effectivity), and G2 and G4 (zero effectivity). Formulae for the force of infection are given elsewhere in this annex.
SIMLEP distinguishes two relapse rates, one for monotherapy, and one for multidrug therapy. The compartment J for individuals who are cured by treatment, and who are immune for new infections, but who can relapse, is split up accordingly: J1 comprises individuals who have been cured by monotherapy (corresponding relapse rate λrelapse1), and J2 reflects cure by multidrug therapy (corresponding relapse rate λrelapse2
Transition rates and probabilities for transitions from compartments
Transitions from most compartments are governed by transitions rates. SIMLEP applies the following transition rates:
λi = rate of leaving the present sub-compartment of asymptomatic infection (i = 1,2)
λheal = rate self-healing from E1 and E2
λdowngr = rate of downgrading from F1 and F2 to G3
λfoiloss = rate of losing capability to transmit M. Leprae lor individuals in G1 and G3
λaware, X, t = rate of becoming aware of disease under the control strategy at time t (X=E1, F1, G1, G2)
λchemo, X, t = rate of reporting for treatment when being aware of disease under the control strategy at time t (X=E2,F2,G3,G4)
λcure, t = cure rate for drug regimen used under control strategy at time t
λrelapse, = relapse rate after dapsone monotherapy cure (relapse occurs from J1)
= relapse rate after dapsone monotherapy cure (relapse occurs from J1)
λrelapse,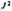 = relapse rate after multidrug therapy cure (relapse occurs from J2)
= relapse rate after multidrug therapy cure (relapse occurs from J2)
SIMLEP is a discrete time simulation model in which people can only make one transition per time step, and in fact calculates transitions according to transition probabilities. For some compartments people can only move to one subsequent compartment. The probability p for occurrence of such a transition during a time step Δt and the corresponding transition rate λ are interrelated tlirough the negative exponential distribution via p = 1 - e -λ-Δt. The corresponding average sojourn time d (in years) in such a compartment is given by d = Δt/p.
For a number of compartments, transitions to different destinations are possible because several events can occur. For these compartments, transition probabilities are derived by combining the negative exponential distribution functions that correspond with the transition rates. The exact formulae for each compartment are given at the end of this annex. Three combination rules are possible:
• the event that takes place first may determine the destination, e.g. self-healing or starting chemotherapy: see the equations for  and
and  .
.
• some events rule out others, e.g. becoming aware of disease is irrelevant if self-healing occurs in the same time step: see the equations for p+eal Ei, and pamlrt Ei,
• events can occur independently of each other in the same time step without excluding each other, e.g. becoming aware of disease and losing effectiveness of contagiousness: see the equations for
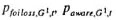 and
and 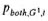
The average sojourn time in compartments from which multiple transitions are possible follows from the sums of the probabilities for these transitions to take place.
Probabilities for determining the destination of transitions which do not depend on transition rates
At birth, people can move to one of several compartments. Similarly, relapses can take place to each of the three types of symptomatic leprosy. The user can specify probabilities that determine the destination of such transitions.
The two chains of subcompartments Dij and D2j represent the slow and fast asymptomatic stages, respectively. The user specified probabilities q-G and qG denote the probability of having a "short" asymptomatic period, i.e. of entering Di,j upon infection. Probability q-G applies to individuals who would eventually move to the compartment G1 and probability qG applies to individuals who would move to one of the other compartments (B,E1,F1 or H). The user also specifies the transition probabilities qDX which denote the probability that newly infected individuals who enter compartment D would eventually transfer to compartment X (X=B,E1,F,G1,H). These individuals may however die during their stay in compartment D. SIMLEP therefore derives probabilities 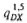 and
and 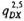 for transfering to compartment X (X=B,E1,F1,G1, H) upon having passed through (and having survived) the five stages of either chain. SIMLEP calculates these probabilities
for transfering to compartment X (X=B,E1,F1,G1, H) upon having passed through (and having survived) the five stages of either chain. SIMLEP calculates these probabilities 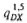 and
and 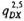 from the probabilities qDX . q-G and qG (X=B,E1,F1,G1,H).
from the probabilities qDX . q-G and qG (X=B,E1,F1,G1,H).
Summarizing, the probabilities which directly determine transition destinations and wliich do not depend on the transition rates are:
q0a = fraction of new borns having (life-long) natural immunity
qcov,t = vaccination coverage among new-borns at time t
qprot,a = protective vaccine efficacy against leprosy infection at age a (qprot,a is a piece-wise linear function of age)
q.G = probability to transfer to D1,1, and hence not to D2,1, upon infection (for a priori destination: B,E1,F1 or H)
qG = probability to transfer to D1,1, and hence not to D2,1, upon infection (for a priori destination: G1)
qDX = user-defined probability of eventually transfering to X after asymptomatic period (X=B,E1,F1,G1,H; 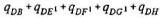 = 1)
= 1)
qall = (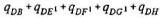 )
) 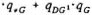
= probability to transfer to D1,1 for an arbitrary newly infected individual

qEX = probability to transfer to X upon self-healing from E1 and E2 (X=B,H; qEB + qEH = 1)
qIX = probability to transfer to X upon treatment cure (X=B,J; qIB + qIJ = 1)
qJX = probability to transfer to X upon relapsing (X=E1,Fl,G1;  = 1)
= 1)
The force of infection
G1 and G3 are by definition contagious, and G2 and G4 are not. Indicator functions indicate wliich of the compartments E1, E2, F1 and F2 have been specified to be (weakly) contagious, and for wliich destinations (E1, F1, G1, and B or H) buildup of contagiousness during the asymptomatic period D has been specified. An initial number of the sub-compartments D1j and D2j can still be specified to be non-contagious when buildup of contagiousness is assumed. The contagiousness is assumed to increase step-wise over the remainder of the five sub-compartments. This is taken care of Uirough the function wbuildup. The force of infection FOIt at time t involves the transmission parameter β, weights for the relative contagiousness of individuals, numbers of individuals in the compartments that are contagious and the total population size Nt at time t. In formula:
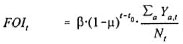
with:
α = age
β = transmission parameter
µ = annual reduction factor for transmission parameter β
t0 = the annual reduction factor p applies from time t0 onwards
w weak = level of contagiousness relative to initial level of contagiousness in G
nb = number of stages out of 5 during which contagiousness builds up in D (0 < nb < 5) (nb = 0 is equivalent to complete absence of contagiousness in D)
 = contagiousness build-up factor for DlJ and D2J:
= contagiousness build-up factor for DlJ and D2J:

iDBH = 0 if those developing asymptomatic infection only are not contagious, 1 otherwise
iDx = 0 if those proceeding to X do not build up contagiousness, 1 otherwise (X=El,F1,G1)
ix = 0 if those in X are (weakly) contagiousness, 1 otherwise
(X=E,F) with E=E1  E2, F=F1
E2, F=F1  F2
F2

The order of calculations for birth, death, ageing and transitions between compartments
At each time step, the compartments are first updated for the transitions that take place between them. Next, the updated compartments are corrected for deatlis that occur during the time step. Then, the age of the remaining (surviving) individuals is increased by one time step, and the new-borns enter into the system with initial age 0. The number of new borns is calculated by multiplying the model parameter b (number of births per head of population per year) with the average of the population sizes before and after death, and with the length of the simulation time step Δt. In the set of difference equations given below a simplified notation is used which does neither express this order of calculations nor the averaging of the population size before and after death for calculating the number of births in the time step.
The set of difference equations for SIMLEP
The following notations are used in the set of difference equations:
t = time
Δt = length of a time step
b = number of births per head of population per year
dc = probability of dying at age a given survival up to age a
a = age
ichemoj = 0 if the drug regimen at time t is dapsone, 1 otherwise
Transition probabilities and transition rates are inter-related as follows:
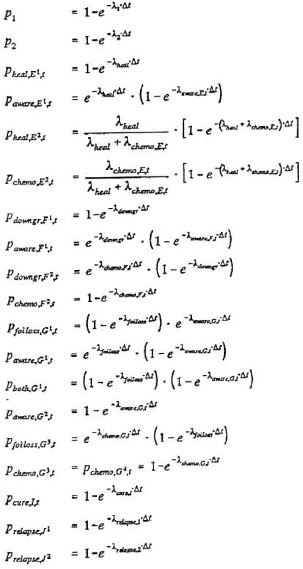
The resulting set of difference equations for SIMLEP is as follows (the superscript1 of the compartments E1,F1 and G1 is omitted in destination probabilities q of transitions to these compartments):
